Discount - 25%
Montgomery Modular Multiplication

Low-Cost High-Performance VLSI Architecture for Montgomery Modular Multiplication

₹9,000.00

Share project:

Source Code : VHDL & VERILOG HDL

Abstract:
This paper proposes a simple and efficient Montgomery multiplication algorithm such that the low-costand high-performance Montgomery modular multiplier can be implemented accordingly. The proposed multiplier output data with representation and uses only one parallel prefix adder to avoid a carry propagation and reduce the area, power and delay, and also increasing the speed. Mainly the usage of parallel prefix adder is to reduce the significant delay reduction and area × time2 improvements, all this at the cost of higher power consumption, which is the main reason preventing the use of parallel-prefix adders to achieve high-speed reverse converters in nowadays systems. Hence, to solve the high power consumption problem, novel specific hybrid parallel-prefix-based adder components those provide better trade-off between delay and power consumption. As a result, the extra clock cycles for operand pre-computation and format conversion can be hidden and high throughput can be obtained. Experimental results show that the proposed Montgomery modular multiplier can achieve higher performance and significant area–time product improvement when compared with previous designs. Using VHDL to design the RTL, and the result to be shown in Xilinx 14.2 with Power consumption and area reduction.

List of the following  materials will be included with the Downloaded Backup:

1. Source code ( Modelsim/ Xilinx/ Quartus/ DSCH3/ Microwind)
2. Existing and Proposed Project Comparison
3. Architecture Diagram
4. Algorithm with Flow chart
5. Report for Phase1 and Phase2
6. Proposed abstract document
7. Reference materials
8. Literature survey with Reference Document
9. Online Support ( Team viewer/ Ammy Admin)



Proposed Title :

FPGA Implementation of Low-Cost and High Performance Montgomery Modular Multiplication with Adaptive Hold Logic based Error Correction 

Improvement of this Project:

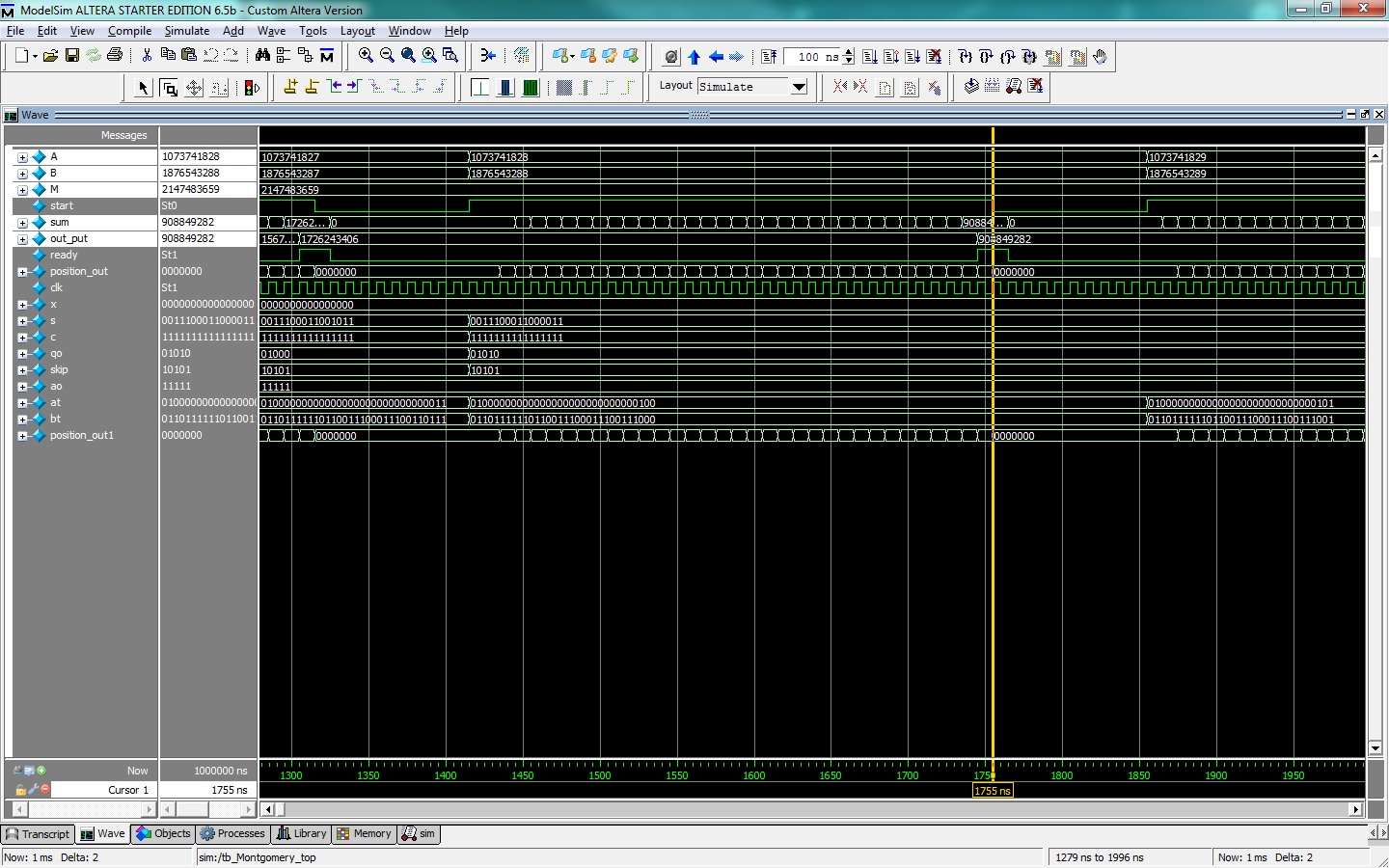
  • In proposed system we are check the output and correct the output if error occurs.  In this system we are use the Adaptive Hold Logic
    (AHL) is to detect and correct the error in the output.

  • To design the 32-Bit Montgomery Modular Multiplication and this Montgomery multiplication integrated with error correction using razor flip flop with support of adaptive hold logic method. 
  • Compared the existing 32-bit Montgomery Modular Multiplication with Proposed 32-bit Montgomery Modular Multiplication in terms of area, delay and power.  

Software implementation:

  • Modelsim
  • Xilinx

” Thanks for Visit this project Pages – Buy It Soon “

LOW Cost High Performance VLSI Architecture for Montgomery Modular Multiplication

Terms & Conditions:

  • Customer are advice to watch the project video file output, before the payment to test the requirement, correction will be applicable.
  • After payment, if any correction in the Project is accepted, but requirement changes is applicable with updated charges based upon the requirement.
  • After payment the student having doubts, correction, software error, hardware errors, coding doubts are accepted.
  • Online support will not be given more than 3 times.
  • On first time explanations we can provide completely with video file support, other 2 we can provide doubt clarifications only.
  • If any Issue on Software license / System Error we can support and rectify that within end of the day.
  • Extra Charges For duplicate bill copy. Bill must be paid in full, No part payment will be accepted.
  • After payment, to must send the payment receipt to our email id.
  • Powered by NXFEE INNOVATION, Pondicherry.

 

Payment Method :

  • Pay Add to Cart Method on this Page
  • Deposit Cash/Cheque on our a/c.
  • Pay Google Pay/Phone Pay : +91 9789443203
  • Send Cheque through courier
  • Visit our office directly
International Payment Method :
 

Bank Accounts

HDFC BANK ACCOUNT:

  • NXFEE INNOVATION,
    HDFC BANK, MAIN BRANCH, PONDICHERRY-605004.
    INDIA,
    ACC NO. 50200013195971,
    IFSC CODE: HDFC0000407.

BUY VLSI PROJECTS ON ON-LINE”
“REFER YOUR FRIENDS WHO WILL NEED VLSI PROJECTS”
“EARN Rs.1,000/- FOR ONE VLSI PROJECT”

(Amount will given After Registration)

Reviews

There are no reviews yet.

Be the first to review “Low-Cost High-Performance VLSI Architecture for Montgomery Modular Multiplication”

Your email address will not be published. Required fields are marked

Related products

sale OFFER 30%
Obfuscating DSP Circuits
,

Obfuscating DSP Circuits via High Level Transformations

₹7,000.00
sale OFFER 40%
Quaternary Logic Lookup Table
,

Quaternary Logic Lookup Table in Standard CMOS

₹6,000.00
sale OFFER 42%
Carry Select Adder
,

Area Delay Power Efficient Carry Select Adder

₹7,000.00
sale OFFER 30%
Loosy Image Compression
,

VLSI-Oriented Lossy Image Compression Approach using DA-Based 2D-Discrete Wavelet

₹14,000.00
sale OFFER 40%
Full Adder
,

Design of 4-bit Ripple carry adder and using 9T full adder

₹6,000.00
sale OFFER 30%
Content Addressable Memory
,

Algorithm and Architecture for a Low Power Content Addressable Memory Based on Sparse Clustered Networks

₹7,000.00
sale OFFER 50%
UHF_RFID
,

ASIC design of UHF RFID reader digital baseband

₹6,000.00

Copyright © 2021 Nxfee Innovation.

Montgomery Modular Multiplication Low-Cost High-Performance VLSI...

₹9,000.00

Home
Shop
0 Cart
More
More