Proposed Title :
FPGA Implementation of Chaos Based Bitwise Dynamical Pseudorandom Number Generator using Galois and Fibonacci series Seed Generation
Improvement of this Project:
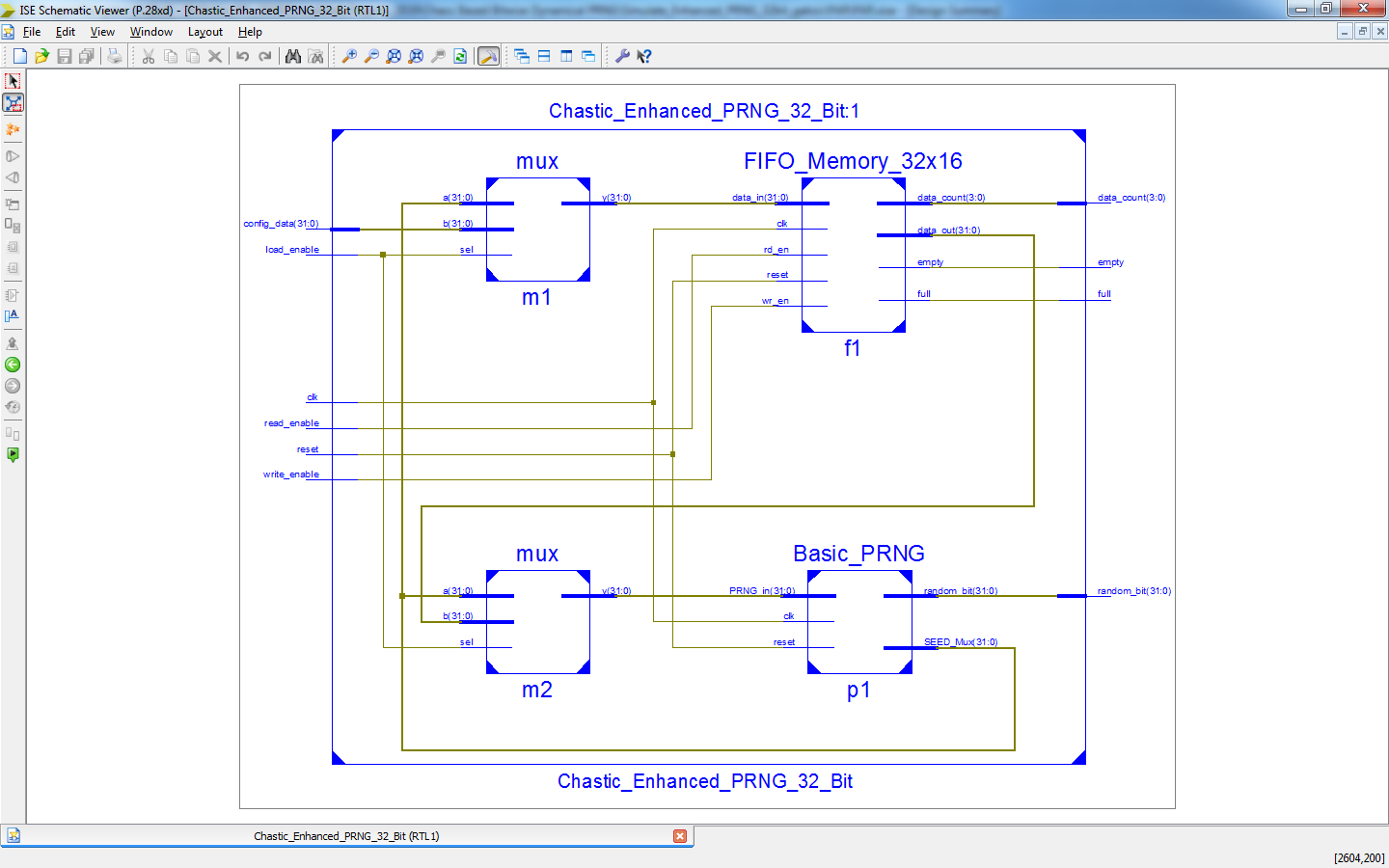
To Design a Enhance PRNG Design with using 8-Bit, 32-Bit FIFO Buffer with 16 Depth size of Galois and Fibonacci LFSR Method of Seed Generation and proved the comparison of Area, Delay and Power.
Software implementation:
- XILINX & MODELSIM
Proposed System:
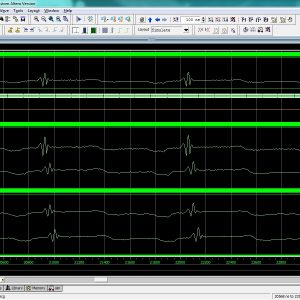
In this work will describe a recent research in cryptography method of Chaos based pseudorandom number generator (PRNG), these method will cooperative in the field of instrumentation and measurements in many applications such as statistical sampling, Monte Carlo simulations, evaluating the immunity to noise of digital systems and communication or procedural generations. The main contribution of this work will presents better randomness results than other PRNG with required very small amount of resources to implementation on FPGA. Here the proposed work will present a two different technique of seed generation in this Enhanced PRNG such as Galois and Fibonacci. This new technique of Galois and Fibonacci will increases better randomness in this Enhanced PRNG and it will take very less resources of area, delay and power. Here, this work will implement in VHDL and simulated in Modelsim and Synthesized in Xilinx FPGA S6LX9-2TQG144 and finally compared all the parameters in terms of area, delay and power.
” Thanks for Visit this project Pages – Buy It Soon “
Chaos-Based Bitwise Dynamical Pseudorandom Number Generator on FPGA
“Buy VLSI Projects On On-Line”
Terms & Conditions:
- Customer are advice to watch the project video file output, before the payment to test the requirement, correction will be applicable.
- After payment, if any correction in the Project is accepted, but requirement changes is applicable with updated charges based upon the requirement.
- After payment the student having doubts, correction, software error, hardware errors, coding doubts are accepted.
- Online support will not be given more than 3 times.
- On first time explanations we can provide completely with video file support, other 2 we can provide doubt clarifications only.
- If any Issue on Software license / System Error we can support and rectify that within end of the day.
- Extra Charges For duplicate bill copy. Bill must be paid in full, No part payment will be accepted.
- After payment, to must send the payment receipt to our email id.
- Powered by NXFEE INNOVATION, Pondicherry.
Payment Method :
- Pay Add to Cart Method on this Page
- Deposit Cash/Cheque on our a/c.
- Pay Google Pay/Phone Pay : +91 9789443203
- Send Cheque through courier
- Visit our office directly
- Pay using Paypal : Click here to get NXFEE-PayPal link