Proposed Title :

CMOS 45nm Implementation of Two Coupled Oscillators with Continuously Controllable Phase Shift

Improvement of this Project:

• • • To change the Technology size of 130nm at 0.9V supply voltage to 45nm at 0.7V supply voltage and proved the comparisons of Area, Delay and Power.

Software implementation:

• TANNER EDA

Proposed System:

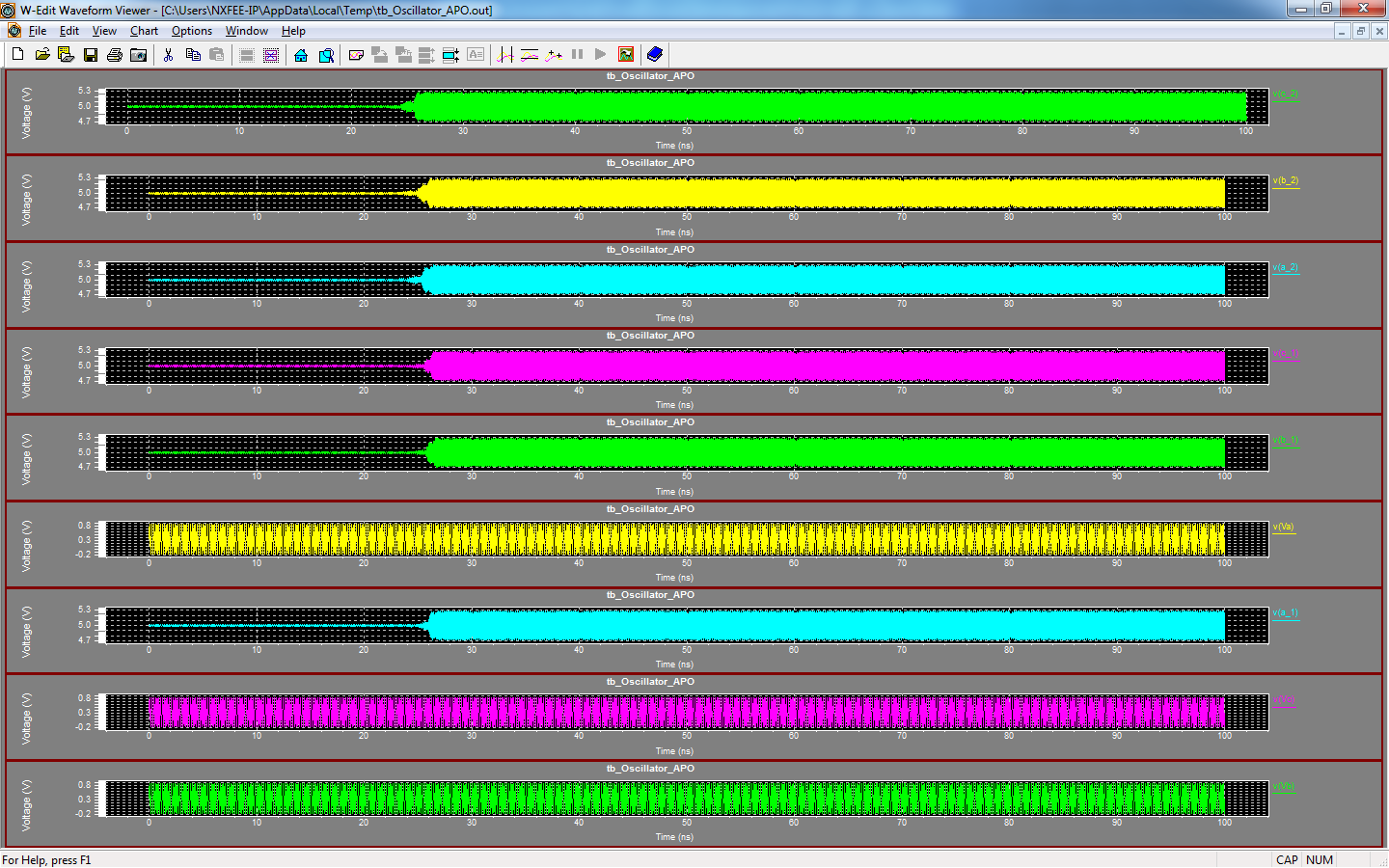
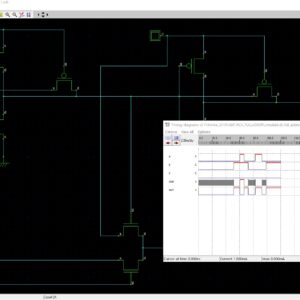
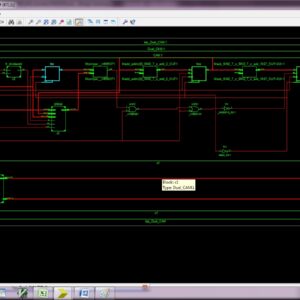
In a recent Methodology of Coupled Oscillator system which have been a numerous applications. Here this work will present a Coupled Oscillator with novel generalization of quadrature oscillators (QVCO) its only generate a phase output at quadrature phases, which present as a Aribitrary phase oscillators (APO) it have a ability to generate any desired phase output. The propsoed structure of this work which present a novel coupling mechanism to generate arbitrary phas shifts between two coupled oscillators without the need of an explicit phase shifter. Here, the proposed work will integrated and verified net list simulation of 130nm at 0.9V supply voltage and 45nm at 0.7V supply voltage with 5GHz Clock Frequency range. The APO structure can be used in designing novel coupled-oscillator-based phased arrays for 5G wireless communications.

” Thanks for Visit this project Pages – Buy It Soon “

A System of Two Coupled Oscillators With a Continuously Controllable Phase Shift

“Buy VLSI Projects On On-Line”