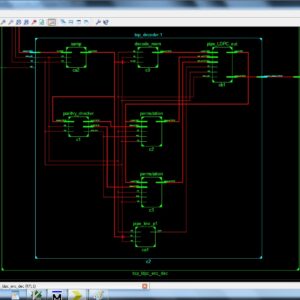
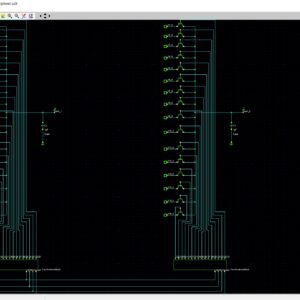
An Efficient VLSI Architecture of Reconfigurable VHBCSE based Pulse Shaping FIR Interpolation
Proposed System:
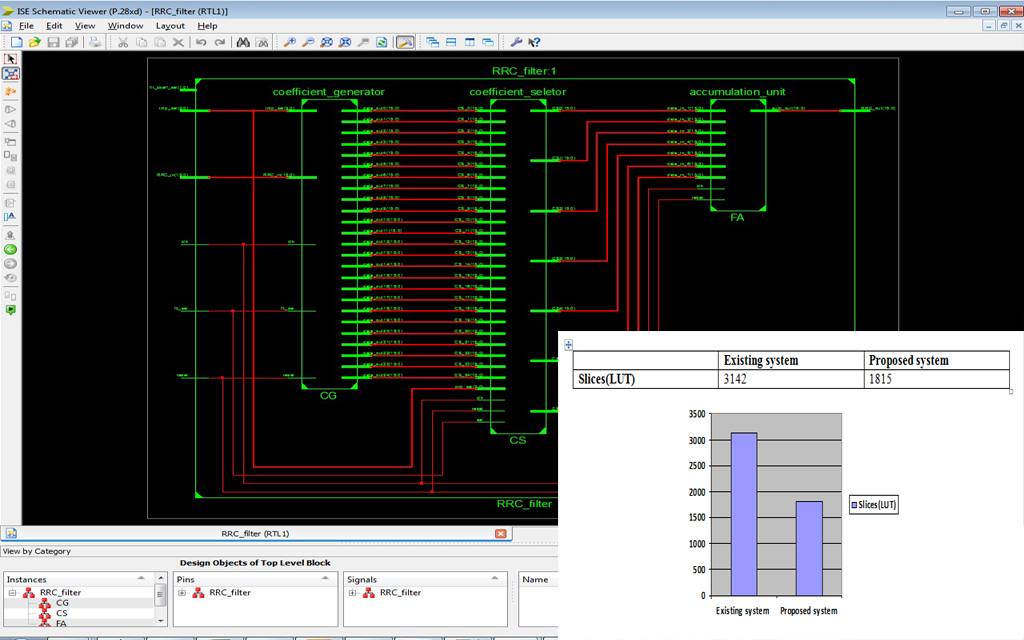
- Use the VHBCSE algorithm for the multiplication process and Increases the Efficiency
Advantages:
- Area coverage is less
- Power consumption is less
Software implementation:
- Modelsim
- Xilinx




Reviews
There are no reviews yet.