Proposed Title :
FPGA Implementation Adiabatic Quantum Flux Parametron technique based 16-Bit BCD adder using Majority Gate
Improvement of this Project:
To implement RCA based BCD adder and CLA based BCD adder using AQFP (Adiabatic Quantum Plux Parametron) majority gate.
• To implement this in 16-bit size of RCA_BCD adder and CFA_BCD adder and shown the parameter value of area, delay and power.
Software implementation:
- Modelsim
- Xilinx 14.2
Proposed System:
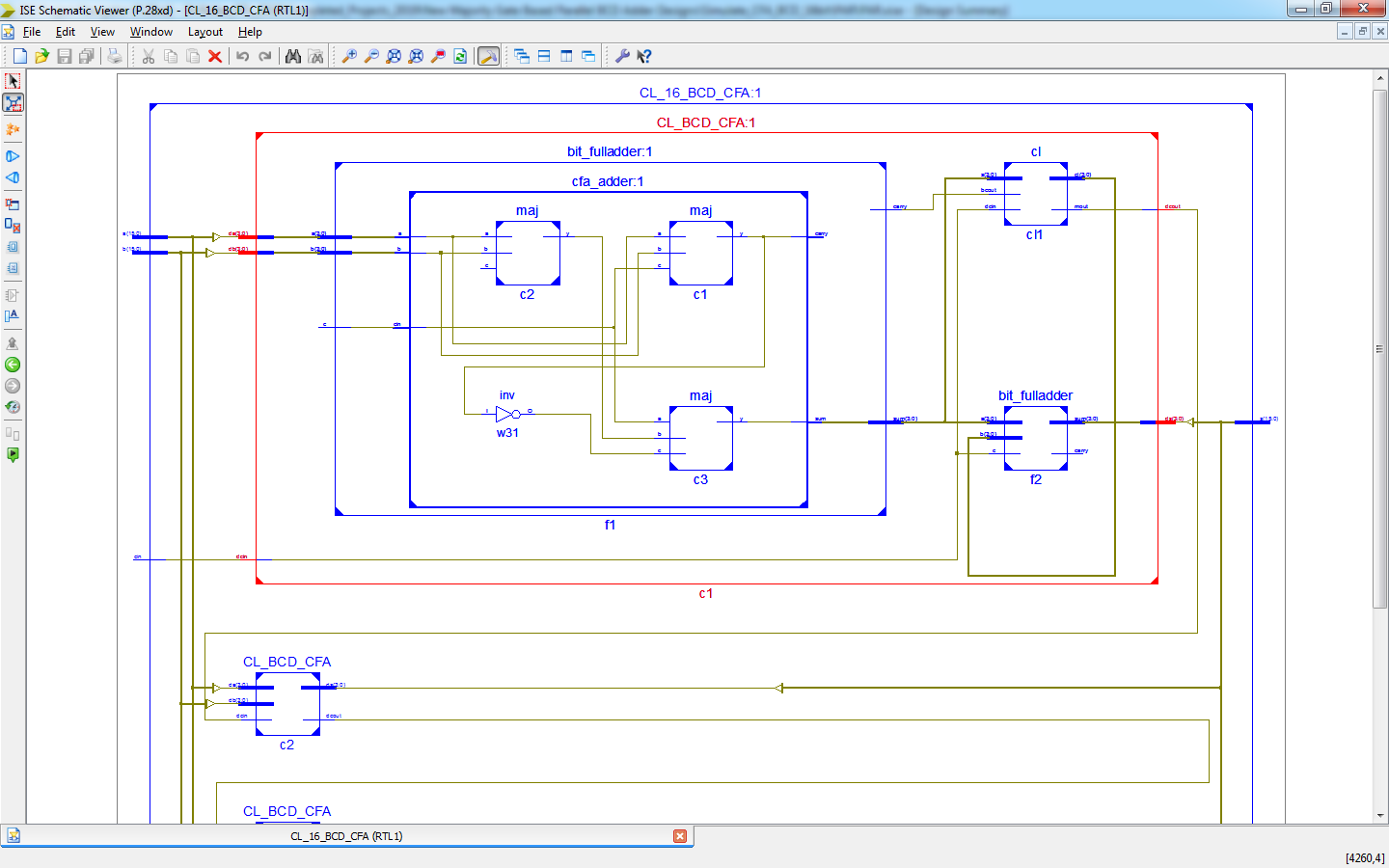
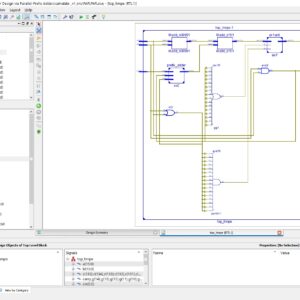
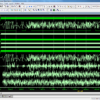
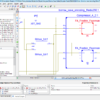
In this recent digital design of BCD (Binary Coded Decimal) adders, which have lot of functionality in digital arithmetic applications, in such as this BCD adder will have lot of complexity in variable bit size and also intermediate carry operations. In existing method of BCD adder will added a Correction logic in between two 4-bit Binary adder, to correct a intermediate Carry operation, with using Majority gate functionality. In this paper we present to reduced the complexity of this BCD adder design which using Adiabatic Qunatum Flux Parametron technique in Majority gate, thus the correction logic operation will improve the performance of area, delay and power, and also reduced the complexity in BCD adders. Here, we are present this BCD adder using RCA (Ripple Carry Adder) and CFA (Carry Flow Adder) methods, in this CFA 1-bit adder will also have Majority gates, thus it will give more performance compared to RCA. Finally this paper presents in VHDL language and Synthesized in Xilinx FPGA S6LX9-2TQ144, and also compared in the terms of area, delay and power.
” Thanks for Visit this project Pages – Buy It Soon “
New Majority Gate Based Parallel BCD Adder Designs for Quantum-dot Cellular Automata
“Buy VLSI Projects On On-Line”
Terms & Conditions:
- Customer are advice to watch the project video file output, before the payment to test the requirement, correction will be applicable.
- After payment, if any correction in the Project is accepted, but requirement changes is applicable with updated charges based upon the requirement.
- After payment the student having doubts, correction, software error, hardware errors, coding doubts are accepted.
- Online support will not be given more than 3 times.
- On first time explanations we can provide completely with video file support, other 2 we can provide doubt clarifications only.
- If any Issue on Software license / System Error we can support and rectify that within end of the day.
- Extra Charges For duplicate bill copy. Bill must be paid in full, No part payment will be accepted.
- After payment, to must send the payment receipt to our email id.
- Powered by NXFEE INNOVATION, Pondicherry.
Payment Method :
- Pay Add to Cart Method on this Page
- Deposit Cash/Cheque on our a/c.
- Pay Google Pay/Phone Pay : +91 9789443203
- Send Cheque through courier
- Visit our office directly
- Pay using Paypal : Click here to get NXFEE-PayPal link