Proposed Title :
FPGA Implementation of Sharing Logic for Built In Generation using 3×3 Circuit under test
Proposed System:
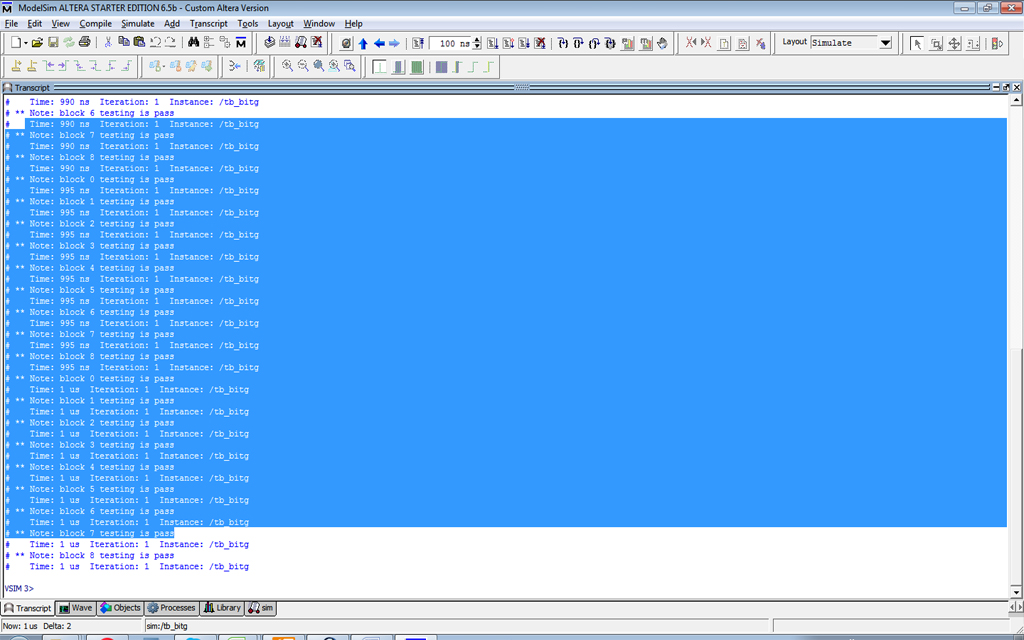
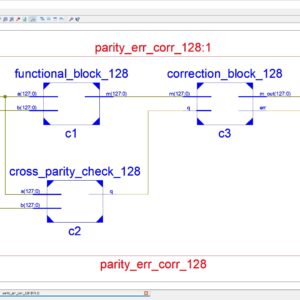
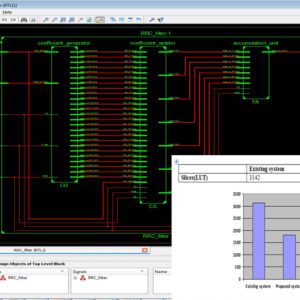
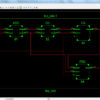
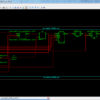
- Sharing Logic for Built In Generation, Increase the number of block in the CUT section up to 9 ( 3×3).
Advantages:
- Easy to identify the similar characteristics for the more block.
Software implementation:
- Model sim
- Xilinx 14.2

Reviews
There are no reviews yet.